The Schrödinger equation (SE) [1], a foundational pillar in quantum mechanics, provides a deep understanding of particle behavior at atomic and subatomic scales. It offers a mathematical description of the quantum scale, revealing insights into the probabilistic nature of particle dynamics and the quantized energy levels within these systems. Notably, the time-independent form of the SE, particularly in many-body systems [2], is pivotal for deciphering complex behaviors in atomic and molecular structures. Solving the many-body SE is a significant challenge in quantum chemistry and condensed matter physics, especially for large systems [3]. The Hamiltonian operator in the SE combines the Laplacian and potential energy terms, making the equation complex to solve analytically for intricate molecules.
DFT [4] is widely employed for analyzing the electronic structures of many-body systems, particularly in atoms, molecules, and condensed phases. DFT simplifies complex calculations by using electron density rather than wave functions, based on the foundational Hohenberg-Kohn theorem [5]. Despite its utility, DFT’s computational load increases exponentially with system size [6]. The method also grapples with accuracy issues due to approximations in electron interaction modeling [7] and challenges in calculating strong electron-electron correlations in materials like transition metal complexes [8, 9, 10]. Further complexities arise in time-dependent DFT applications for excited states and optical properties [11, 12, 13, 14], and electron repulsion adds to the intricacy in electronic structure calculations [15]. While beneficial, DFT faces scalability and precision issues in complex materials [16, 17].
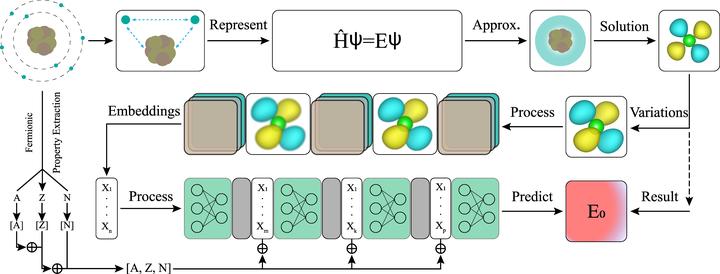
In addressing existing challenges in materials science, this work introduces a novel physics-informed [18], vision-based deep learning model, QuantumShellNet, designed for swift and precise prediction of ground-state eigenvalues in materials. QuantumShellNet begins by approximating the system’s Hamiltonian for electronic structure derivation. This structure, transformed into a standardized image format, is then fed into an orbital encoder convolutional neural network (CNN). The model subsequently utilizes an atomic multilayer-perceptron (AMLP) block, integrating key material properties, for predictions. With approximately 235,000 parameters, QuantumShellNet excels in computational efficiency, surpassing traditional DFT and advanced ML models like FermiNet [19] and PsiFormer [20].

Key contributions of this work include: (i) the introduction of an orbital-to-vector approach that significantly improves computational efficiency by reducing from higher orders to O(1) [21] and decreasing training time; (ii) the development of the AMLP model for accurate predictions of total energies of elements and molecules using orbital vectors; and (iii) an enhanced capability for predicting unseen materials, providing new insights into various systems.
Cite this article (BibTeX – Soon):
@article{polat2025quantumshellnet,
title={QuantumShellNet: Ground-state eigenvalue prediction of materials using electronic shell structures and fermionic properties via convolutions},
author={Polat, Can and Kurban, Hasan and Kurban, Mustafa},
journal={Computational Materials Science},
volume={246},
pages={113366},
year={2025},
publisher={Elsevier}
}References
[1] Schrödinger, E. An Undulatory Theory of the Mechanics of Atoms and Molecules. Physical Review 1926, 28, 1049.
[2] Shankar, R. Principles of Quantum Mechanics; Springer Science & Business Media, 1994.
[3] Bruus, H.; Flensberg, K. Many-body Quantum Theory in Condensed Matter Physics: An Introduction; OUP Oxford, 2004.
[4] Sholl, D. S.; Steckel, J. A. Density Functional Theory: A Practical Introduction; John Wiley & Sons, 2022.
[5] Kohn, W.; Sham, L. J. Self-Consistent Equations Including Exchange and Correlation Effects. Physical Review 1965, 140, A1133.
[6] Goedecker, S. Linear Scaling Electronic Structure Methods. Rev. Mod. Phys. 1999, 71, 1085–1123.
[7] Goedecker, S.; Teter, M.; Hutter, J. Separable Dual-Space Gaussian Pseudopotentials. Phys. Rev. B 1996, 54, 1703–1710.
[8] Bisti, F.; Rogalev, V. A.; Karolak, M.; Paul, S.; Gupta, A.; Schmitt, T.; Güntherodt, G.; Eyert, V.; Sangiovanni, G.; Profeta, G.; Strocov, V. N. Weakly-Correlated Nature of Ferromagnetism in Nonsymmorphic CrO₂ Revealed by Bulk-Sensitive Soft-X-Ray ARPES. Phys. Rev. X 2017, 7, 041067.
[9] Taranto, C.; Kaltak, M.; Parragh, N.; Sangiovanni, G.; Kresse, G.; Toschi, A.; Held, K. Comparing Quasiparticle GW+DMFT and LDA+DMFT for the Test Bed Material SrVO₃. Phys. Rev. B 2013, 88, 165119.
[10] Mandal, S.; Haule, K.; Rabe, K. M.; Vanderbilt, D. Electronic Correlation in Nearly Free Electron Metals with Beyond-DFT Methods. npj Computational Materials 2022, 8, 181.
[11] Elliott, P.; Furche, F.; Burke, K. Reviews in Computational Chemistry; John Wiley & Sons, Ltd, 2008; Chapter 3, pp 91–165.
[12] Baer, R.; Neuhauser, D. Theoretical Studies of Molecular Scale Near-Field Electron Dynamics. The Journal of Chemical Physics 2006, 125, 074709.
[13] Livshits, E.; Baer, R. Time-Dependent Density-Functional Studies of the D₂ Coulomb Explosion. The Journal of Physical Chemistry A 2006, 110, 8443–8450.
[14] Band, Y.; Kallush, S.; Baer, R. Rotational Aspects of Short-Pulse Population Transfer in Diatomic Molecules. Chemical Physics Letters 2004, 392, 23–27.
[15] Simons, J. Why Is Quantum Chemistry So Complicated? Journal of the American Chemical Society 2023, 145, 4343–4354.
[16] Becke, A. D. Perspective: Fifty Years of Density-Functional Theory in Chemical Physics. The Journal of Chemical Physics 2014, 140.
[17] Szabo, A.; Ostlund, N. S. Modern Quantum Chemistry: Introduction to Advanced Electronic Structure Theory; Courier Corporation, 2012.
[18] Karniadakis, G. E.; Kevrekidis, I. G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-Informed Machine Learning. Nature Reviews Physics 2021, 3, 422–440.
[19] Pfau, D.; Spencer, J. S.; Matthews, A. G. D. G.; Foulkes, W. M. C. Ab-Initio Solution of the Many-Electron Schrödinger Equation with Deep Neural Networks. Physical Review Research 2020, 2, 33429.
[20] von Glehn, I.; Spencer, J. S.; Pfau, D. A Self-Attention Ansatz for Ab-Initio Quantum Chemistry. 2022.
[21] Press, W. H. The Art of Scientific Computing; Cambridge University Press, 1992.

 DOI
DOI Code
Code Data
Data